Category: Music Theory
Lecture 4 of the Nature of Music Gresham Lecture Series.
Release of Perks & McGrath edited collection of contemporary guitar research. A wonderful project to be involved with (contributing a chapter on ‘The Digital Fretboard) and design the cover)

In the 21st Century, the guitar, as both a material object and tool for artistic expression, continues to be reimagined and reinvented. From simple adaptations or modifications made by performers themselves, to custom-made instruments commissioned to fulfil specific functions, to the mass production of new lines of commercially available instruments, the extant and emergent forms of this much-loved musical instrument vary perhaps more than ever before. As guitars sporting multiple necks, a greater number of strings, and additional frets become increasingly common, so too do those with reduced registers, fewer strings, and fretless fingerboards. Furthermore, as we approach the mark of the first quarter-century, the role of technology in relation to the guitar’s protean nature is proving key, from the use of external effects units to synergies with computers and AR headsets. Such wide-ranging evolutions and augmentations of the guitar reflect the advancing creative and expressive needs of the modern guitarist and offer myriad new affordances.
21st Century Guitar examines the diverse physical manifestations of the guitar across the modern performative landscape through a series of essays and interviews. Academics, performers and dual-practitioners provide significant insights into the rich array of guitar-based performance practices emerging and thriving in this century, inviting a reassessment of the guitar’s identity, physicality and sound-creating possibilities.
https://www.bloomsbury.com/uk/21st-century-guitar-9781501373305/
An investigation of how music conveys and triggers such a range and depth of emotion. Featuring the BRECVEMA (aka EVERBEAM X) model of music psychology.
References:
Juslin & Västfjall, ‘Emotional responses to music: The need to consider underlying mechanisms, Behavioral and Brain Sciences, 31, 2008; 559-621.
Juslin, Liljeström, Västfjäll, & Lundqvist. (2010). How does music evoke emotions? Exploring the underlying mechanisms. In P.N. Juslin & J. Sloboda (Eds.), Handbook of Music and Emotion: Theory, Research, and Applications (pp. 605-642). Oxford: Oxford University Press.
Huron, D. (2006). Sweet anticipation: Music and the psychology of expectation. MIT Press
Pieces include:
QED Theme, Corale – Mermikides, M.
Small Comfort – George Hrab
“Hidden music” is a talk given in the interdisciplinary seminar series on Eudaimonia and Human Flourishing on 24.05.2022 at Linacre College, Oxford University. The talk is in two conceptual halves: The nature of music and the music of nature. For info and to watch the talk click below.
A short, deep dive into harmonic consonance and dissonance and an understanding of harmonic flavour and spiciness. Dissonance curves, interval classes, vectors, All-interval tetrachords and introducing the Harmonic Scoville (or Scofield?) Scale.
This video reveals the beautifully interconnected symmetry of the diatonic modes, three entwined cycle of rotation, brightness and reflection in a single compass. Further Reading/Sources: Touissaint’s original Euclidean paper (concerning rhythms but relevant here): http://cgm.cs.mcgill.ca/~godfried/pub… Persichetti’s quite awesome and insightful ’20th century harmony’: https://www.academia.edu/38883692/Vin…
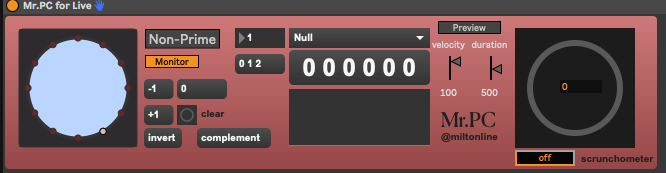
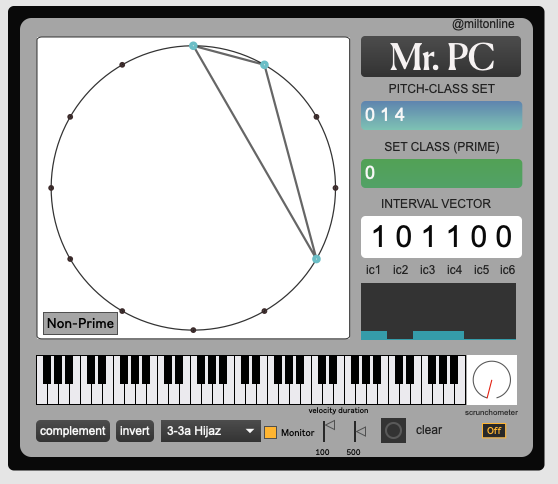
Every chord in the (12TET) Universe – a gentle introduction to Pitch-class Set Theory.
To download the Mr. PC patches (for Max/MSP standalone and Max for Live click below. Note: 1) they both need the excellent and free Bach package by A. Agostini & D. Ghisi (installable in Max’s Package manager) consider donating (to them). 2) For Apple Silicon computers, Max needs to be running under Rosetta. 3) These are good enough tools for teaching and music adventure – use at your own theoretical risk.
A cosmic view of the earthly and unassuming diatonic scale.
IGRC22

The IGRC are delighted to announce the International Guitar Research Centre Conference 7th to 9th October 2022
REGISTER HERE
For information: http://IGRC.site/IGRC22
It’s privilege to present the Keynote for the Guitar Foundation of America convention this year.

The event runs June 26, 2022,5 PM – 9:30 PM UTC+01 on Zoom (register to join)You are warmly invited to join us for a series of discussions with scholars from Brazil, the United States, Switzerland, and England. Attendees will have the opportunity to speak informally with the presenters or simply listen. Registration is required. Abstract below:
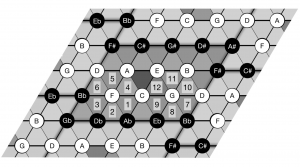
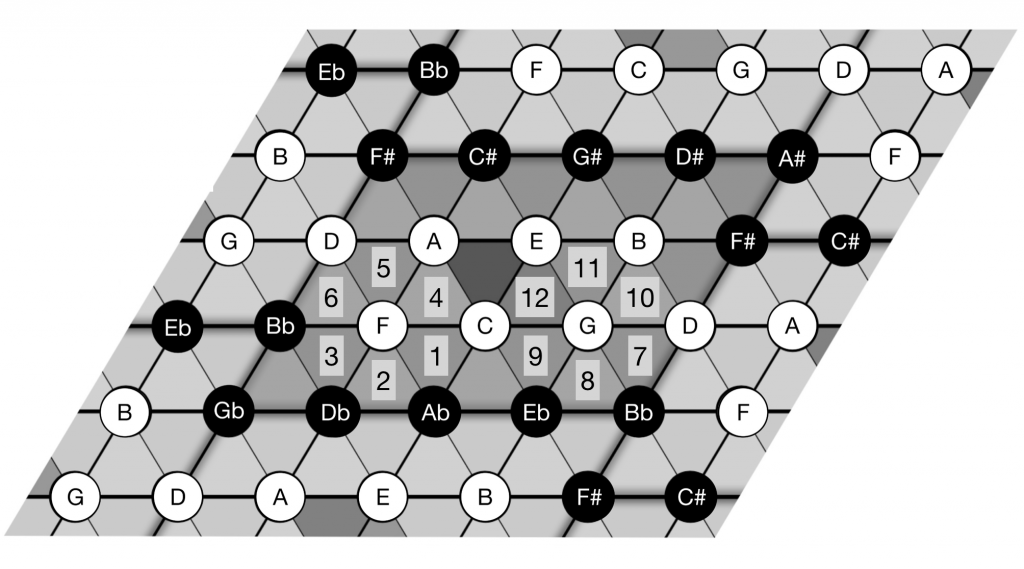
Diamonds, Abaci, and Hexagrams: Exploring the Pitch Surface of the Guitar Fretboard
In this presentation, I will analyze the idiosyncrasies, challenges, limits, and affordances of the guitar’s “pitch surface”: its fretboard and tuning. Whatever the context—staff notation, music theory, improvisation, performance, and other arenas of guitar activity—the layout of the fretboard exerts a profound influence on how guitarists learn, play, and compose. Inspired by De Souza, Goodrick, and Martino, I will also explore the benefits of creative constraints: scordatura, capo, MIDI tools, and other ways of remapping the guitar’s pitch matrix. These constraints can be used to break the guitarist’s tight auditory-motor link, revitalizing the fretboard as a primary musical space and insightful musical “abacus.”
J.S.Bach in Aeon
My essay on J.S.Bach’s crafty brilliance and its implications for us all is now published in the wonderful Aeon digital magazine. Many thanks to Nigel Warburton (author, philosopher and podcaster) for the commissioning, editing and constant support.

https://aeon.co/essays/look-into-the-secret-world-of-numerology-and-puzzles-in-bach

It was fun writing this track-by-track musicological analysis of Led Zep IV (50 this year ahem) for the cover feature of Classic Rock Magazine. Limited by copyright and terminology, it’s challenging and instructive to communicate deep theory without dumbing down. Also I now know how to hear the beginning of Rock n Roll and the bridge of Stairway. Get it here and all reasonable shops.

Musical illustrations of Arvo Pärt’s Spiegel im Spiegel and Beatitudes are now published in Arvo Pärt’s Resonant Texts: Choral and Organ Music 1956–2015 (Shenton 2018) and Illiano, R., & Locanto, M. (Eds.). (2019). Twentieth-century music and mathematics. Brepols.
These unpack the musical mechanisms of Arvo Pärt’s music as outlined in this lecture below.
Anatomy of a Guitar Solo
Originally commissioned for Total Guitar, this examination of the reader-voted top 50 guitar solos is now publicly available on Guitar World.
A live video presentation at the fantastic 21st Century Guitar Conference “in” Lisbon, March 2021, hosted by the wonderful Amy Brandon and Rita Torres. ‘Digital Self-Sabotage’ explores we guitarists’ deep and twisted engagement with the fretboard, and how technology can expand and disrupt this bond for learning and insight.
Soundboard Scholar (No.6) features my paper. “Monitored Freedom: Swing Rhythm in the Jazz Arrangements of Roland Dyens” examines the time-feel in the performances and scores of Roland Dyens, in particular reference to his arrangement of Nuages – and Django’s performances of this piece. Working with the genius Jonathan Leathwood is always a privilege and joy, and I am very grateful that my illustration is used as the cover image to the journal. Available here.

Pleasing to see my ‘postcard’ analyses of Arvo Pärt’s Beatitudes and Spiegel Im Spiegel published in Andrew Shenton’s fine new work Arvo Pärt’s Resonant Texts (Cambridge University Press).
Here they are without explanation.
A lovely discussion with BBC Studio Manager (and Radiophonic scholar) Jo Langton and presenter Tom Service on Radio 3’s Hidden Voices series on Music Matters. Kathleen Schlesinger’s The Greek Aulos, Ancient Greek Modes, microtonality, the work of Elsie Hamilton and its legacy today.
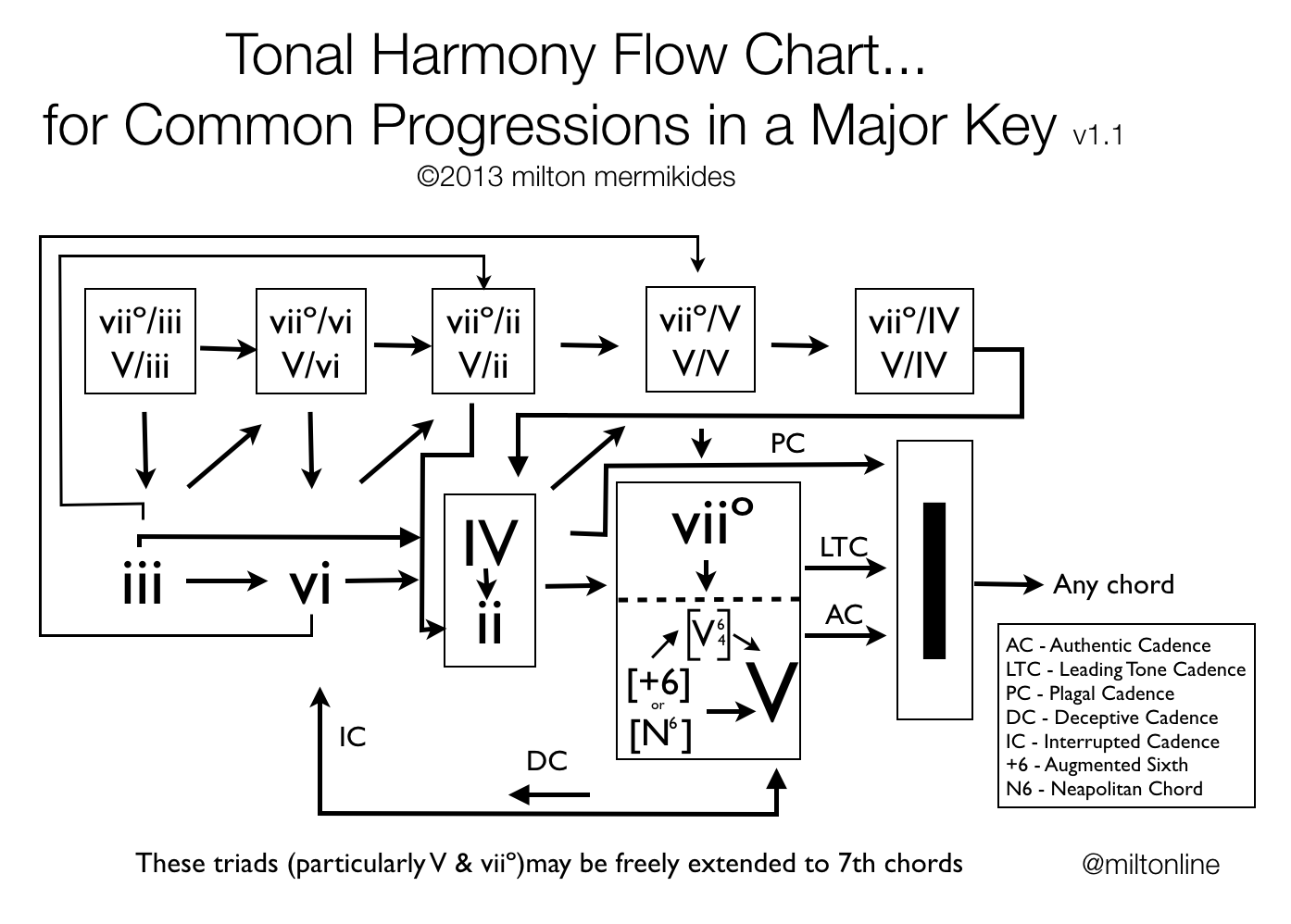
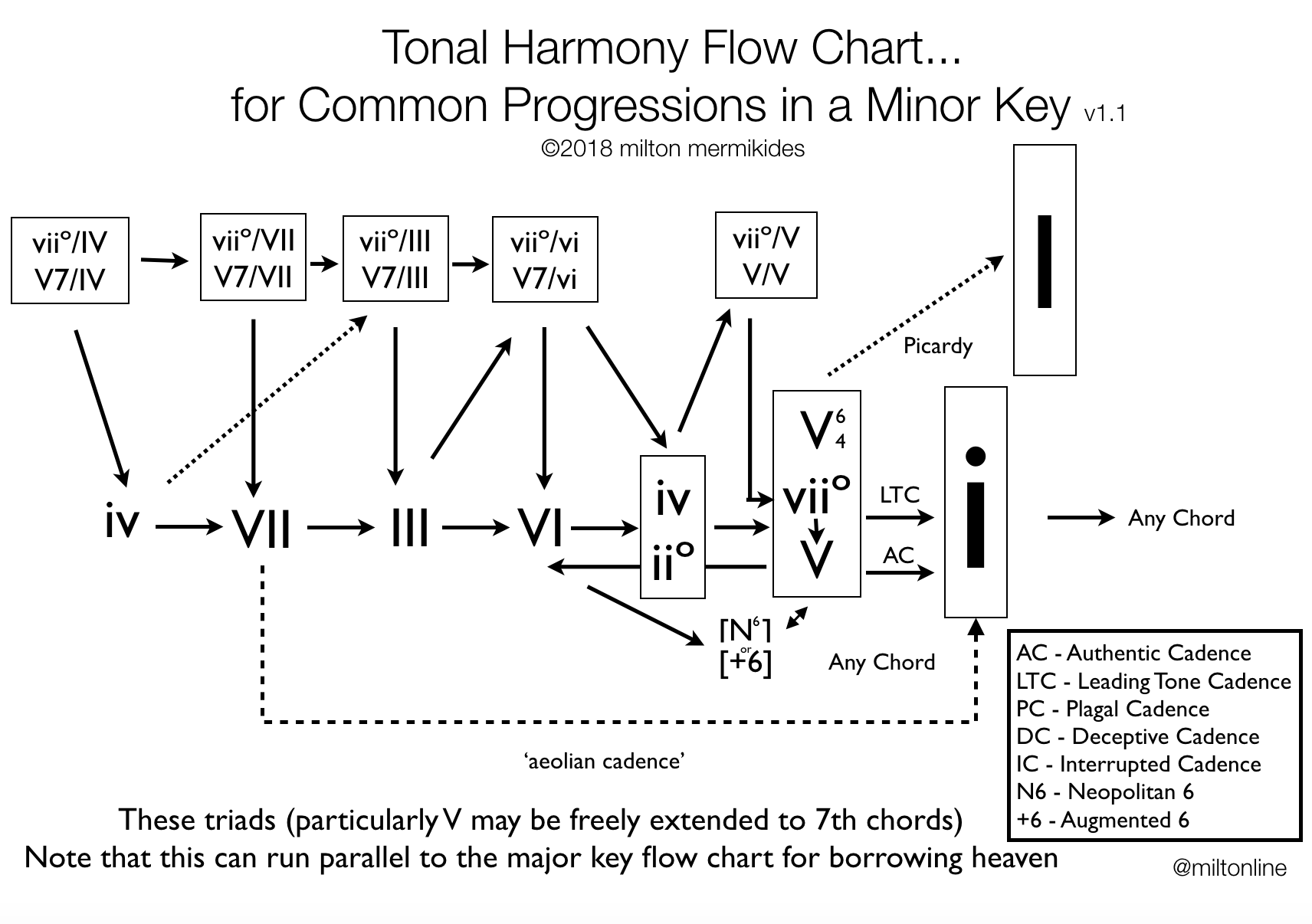
By (heavily belated) popular demand here’s a stab at ‘common-practice’ chord progressions in major and now minor keys!
Really looking forward to being on this fabulous panel at the fabulous QED conference in fabulous Manchester. Panel on 14th October 2018 Time TBC
Truth Hertz – join @Rick_Owen, @carmenego, Ann-Marie Cundy, @miltonline and @sophiescott as they reflect some of the wisdom of science on the mystics of music, the audiophiles and the numerologists at #QEDCon2018 https://t.co/cjcifOrSLf pic.twitter.com/nXQDZJADSq
— QED (@QEDcon) October 6, 2018
Trying to push my Push skills up a peg with Peg and Steely Dan’s gorgeous µ harmonies.