Lecture 4 of the Nature of Music Gresham Lecture Series.
Category: Learning & Teaching
The first of the 6-part Gresham College Lecture Series, delivered at LSO St. Luke’s, Sep 14 2023. Now on YouTube. Transcript.
I am excited and honoured to be appointed the 37th Gresham Professor of Music, and the rich opportunity to share music knowledge it affords. This is a post that has been running since 1597 – offering (thanks to the will of Thomas Gresham) free public lectures to all – and to inherit the professorship from the likes of John Bull, Iannis Xenakis and Joanna MacGregor is quite surreal. I’ll be giving six public lectures a year which you can attend live, watch on live-stream or after the event. Details on the 2023-24 Lecture Series – The Nature of Music are here
Forget all my moon phases and compasses, this is super useful practical tips to compose with modes. 7 tips to use in your compositions of any style.
An investigation of how music conveys and triggers such a range and depth of emotion. Featuring the BRECVEMA (aka EVERBEAM X) model of music psychology.
References:
Juslin & Västfjall, ‘Emotional responses to music: The need to consider underlying mechanisms, Behavioral and Brain Sciences, 31, 2008; 559-621.
Juslin, Liljeström, Västfjäll, & Lundqvist. (2010). How does music evoke emotions? Exploring the underlying mechanisms. In P.N. Juslin & J. Sloboda (Eds.), Handbook of Music and Emotion: Theory, Research, and Applications (pp. 605-642). Oxford: Oxford University Press.
Huron, D. (2006). Sweet anticipation: Music and the psychology of expectation. MIT Press
Pieces include:
QED Theme, Corale – Mermikides, M.
Small Comfort – George Hrab
A short, deep dive into harmonic consonance and dissonance and an understanding of harmonic flavour and spiciness. Dissonance curves, interval classes, vectors, All-interval tetrachords and introducing the Harmonic Scoville (or Scofield?) Scale.
This video reveals the beautifully interconnected symmetry of the diatonic modes, three entwined cycle of rotation, brightness and reflection in a single compass. Further Reading/Sources: Touissaint’s original Euclidean paper (concerning rhythms but relevant here): http://cgm.cs.mcgill.ca/~godfried/pub… Persichetti’s quite awesome and insightful ’20th century harmony’: https://www.academia.edu/38883692/Vin…
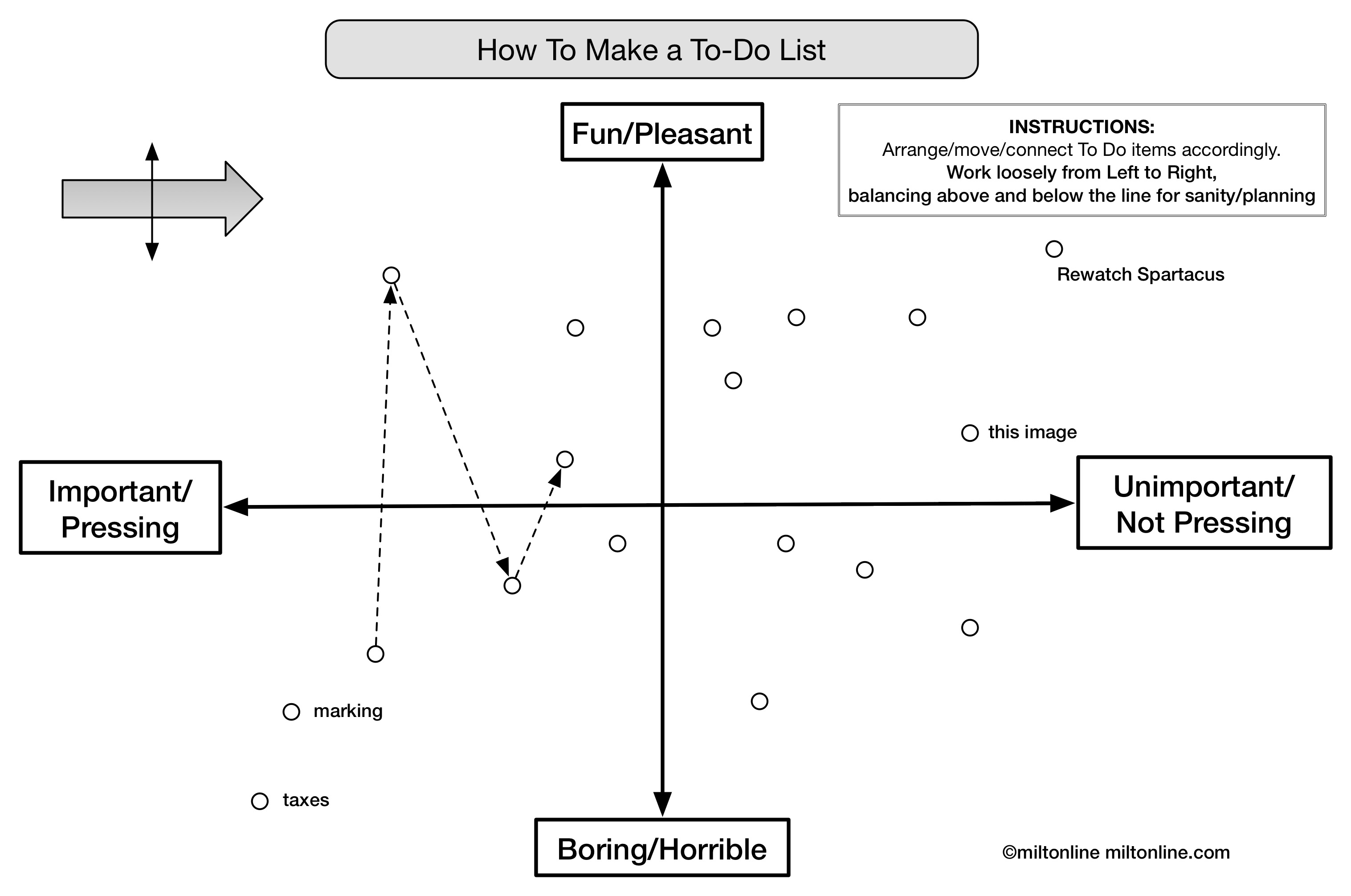
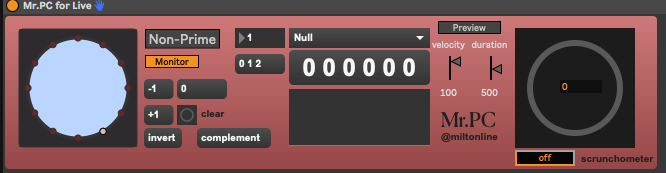
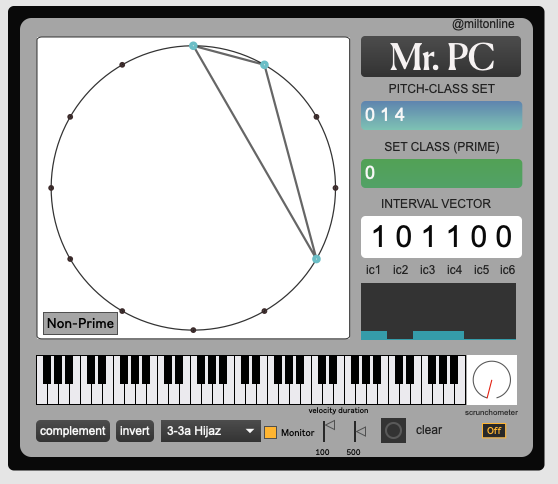
Every chord in the (12TET) Universe – a gentle introduction to Pitch-class Set Theory.
To download the Mr. PC patches (for Max/MSP standalone and Max for Live click below. Note: 1) they both need the excellent and free Bach package by A. Agostini & D. Ghisi (installable in Max’s Package manager) consider donating (to them). 2) For Apple Silicon computers, Max needs to be running under Rosetta. 3) These are good enough tools for teaching and music adventure – use at your own theoretical risk.
A cosmic view of the earthly and unassuming diatonic scale.
It’s privilege to present the Keynote for the Guitar Foundation of America convention this year.
The event runs June 26, 2022,5 PM – 9:30 PM UTC+01 on Zoom (register to join)You are warmly invited to join us for a series of discussions with scholars from Brazil, the United States, Switzerland, and England. Attendees will have the opportunity to speak informally with the presenters or simply listen. Registration is required. Abstract below:
Diamonds, Abaci, and Hexagrams: Exploring the Pitch Surface of the Guitar Fretboard
In this presentation, I will analyze the idiosyncrasies, challenges, limits, and affordances of the guitar’s “pitch surface”: its fretboard and tuning. Whatever the context—staff notation, music theory, improvisation, performance, and other arenas of guitar activity—the layout of the fretboard exerts a profound influence on how guitarists learn, play, and compose. Inspired by De Souza, Goodrick, and Martino, I will also explore the benefits of creative constraints: scordatura, capo, MIDI tools, and other ways of remapping the guitar’s pitch matrix. These constraints can be used to break the guitarist’s tight auditory-motor link, revitalizing the fretboard as a primary musical space and insightful musical “abacus.”
Categories
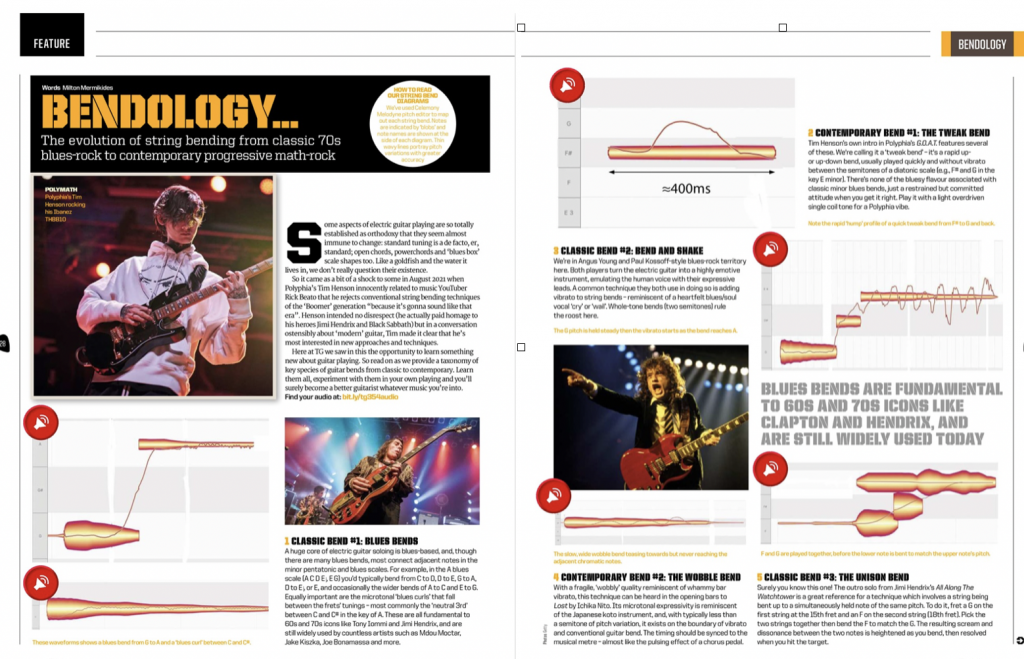
Bendology in Total Guitar
It was fun putting together this article with Chris Bird for Total Guitar (Feb 2022), and using the whole BoomerBendGate as an opportunity for some bendological research. In so doing discovered some ridiculously killer zoomer players in Tim Henson, Mateus Asato, Wes Hauch, Ichiko Nito, Plini and all.
And is now published online in Guitar World
Categories
John Mayer in GT
My article on the remarkable John Mayer’s Blues techniques is the cover feature of Guitar Techniques GT328. Read it and (make your guitar) weep.
Categories
Lessons from Eurovision
Total Guitar (Issue 345) has published an article on what Eurovision teaches us about music listening, and (guitar) performance. Some sample images below on rhythmic, perception, tempo and modulation respectively.
My article providing practical insights into the music and playing of the late, great Allan Holdsworth is now available for public free consumption on MusicRadar (including notation & audio). A teaser below.
A breakdown of the musical science of the Sea Shanty in Total Guitar Issue 344
Engaging directly with time-feel and micro-timing on the electric guitar with specific exercises and style studies. This is for many levels of player who wants to draw focus to the elements of groove which are often excluded, glossed over or mythologized in the learning process.
Soundboard Scholar (No.6) features my paper. “Monitored Freedom: Swing Rhythm in the Jazz Arrangements of Roland Dyens” examines the time-feel in the performances and scores of Roland Dyens, in particular reference to his arrangement of Nuages – and Django’s performances of this piece. Working with the genius Jonathan Leathwood is always a privilege and joy, and I am very grateful that my illustration is used as the cover image to the journal. Available here.
A pleasure to indulge in full-tilt nerdery about micro-timing with the annoyingly talented and annoyingly nice hosts of The Guitar Hour Podcast. \m/ \m/
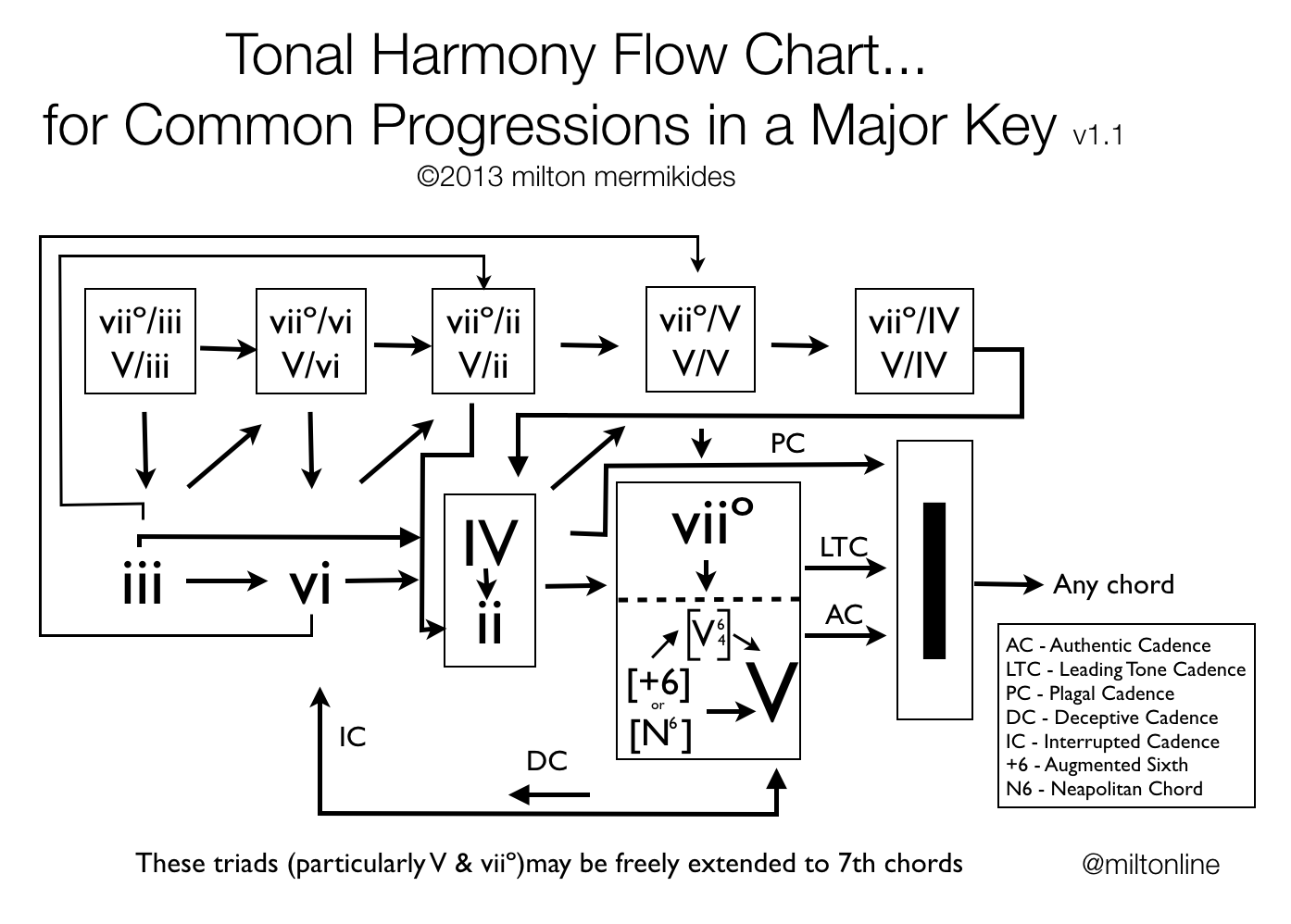
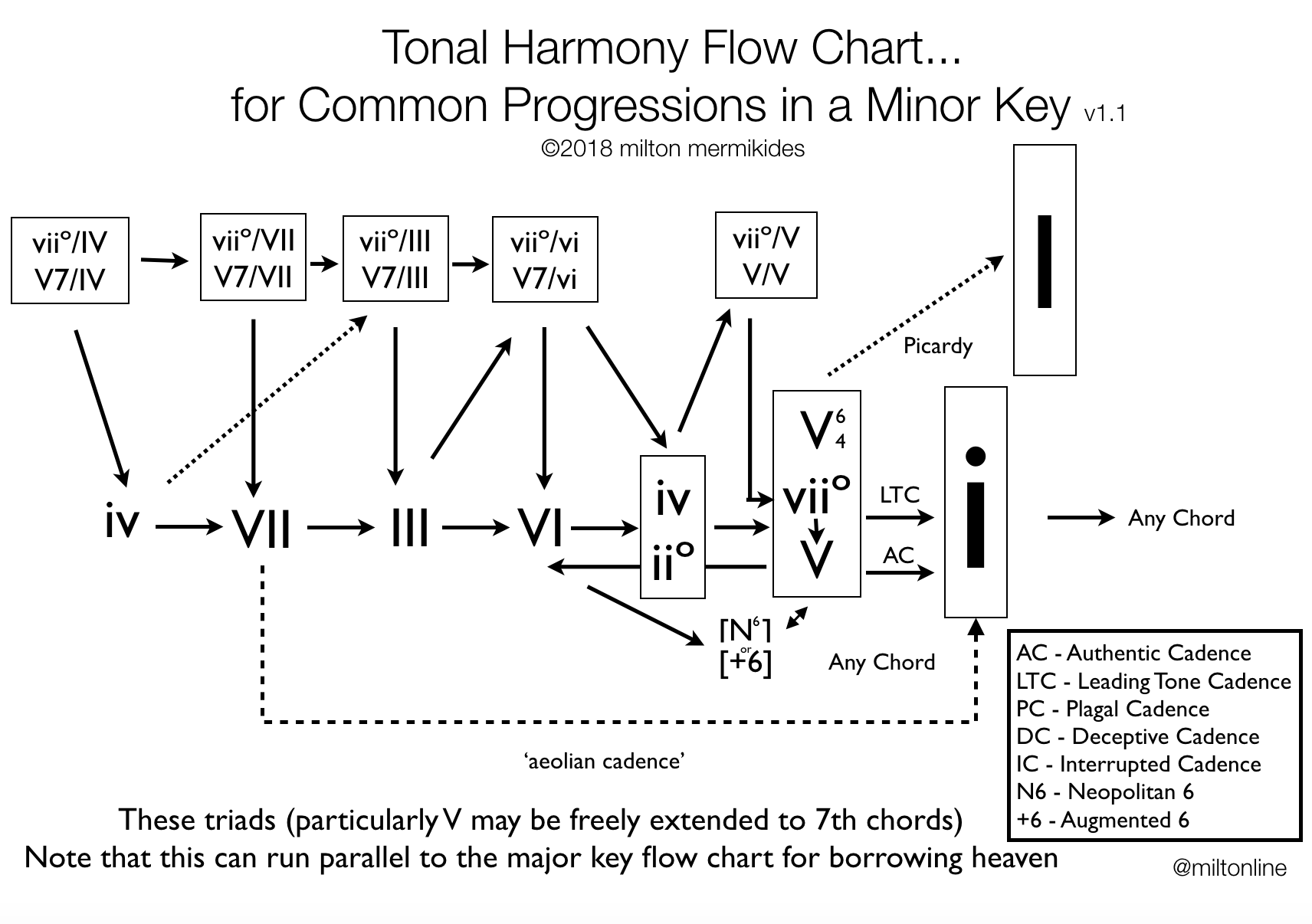
By (heavily belated) popular demand here’s a stab at ‘common-practice’ chord progressions in major and now minor keys!
Am looking forward to this event and the opportunity to do something different and fun with the excellent Ensemble Montage.
Milton Mermikides & Ensemble Montage | Hidden Music
What does the skyline of New York sound like? How can you make a composition from your sleep patterns or blood cells? Music can be made from anything we find around us, from our names or birth dates to our cells, from atoms to stars. Composer and guitarist Milton Mermikides presents the fascinating origins and history of data sonification – the translation of information or patterns into sound and music – as well as a selection of his own compositions derived from sleep cycles, viruses, paintings, exoplanetary moons, traffic patterns and other ‘non-musical’ data. In addition, a string trio of the Ensemble Montage will demonstrate how these data sound and perform a new composition based on ‘the hidden music’ of Noorderzon Performing Arts Festival. Discover how music can reveal the patterns in the natural world, and give us both a theoretical and aesthetic appreciation of everything around us.
For students and subscribers of Studium Generale tickets are € 5,-
