Harmonic Series vs. 12-Tone Equal Temperament

It’s hard (for me at least) to start talking about any aspect of musical theory without talking for an hour or writing several thousand words and/or producing many diagrams. So I’m going to try and just provide some vignette posts, little moments of insight in a hugely complex field of study.
Here let’s look at the harmonic series (the pitches that emerge by multiplying a frequency by the set of integers (1,2,3,4 …) and its relationship to 12-tone equal temperament (the ‘standard’ division of the octave into 12 equal divisions).
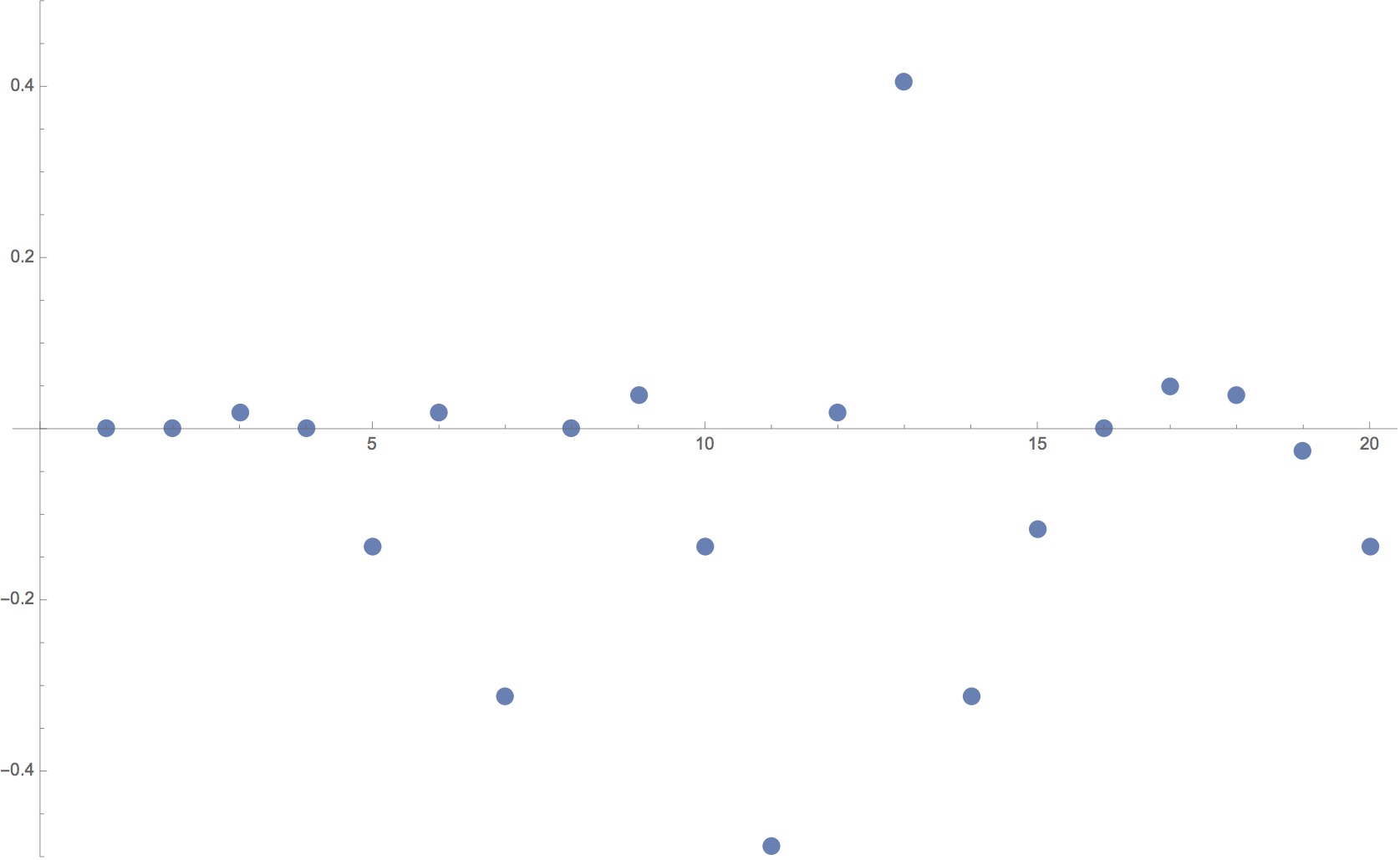
The following diagram courtesy of the incredible programmer Dean McNamee (and Mathematica) shows how the pitches generated through the harmonic series differ from 12-tone equal temperament.

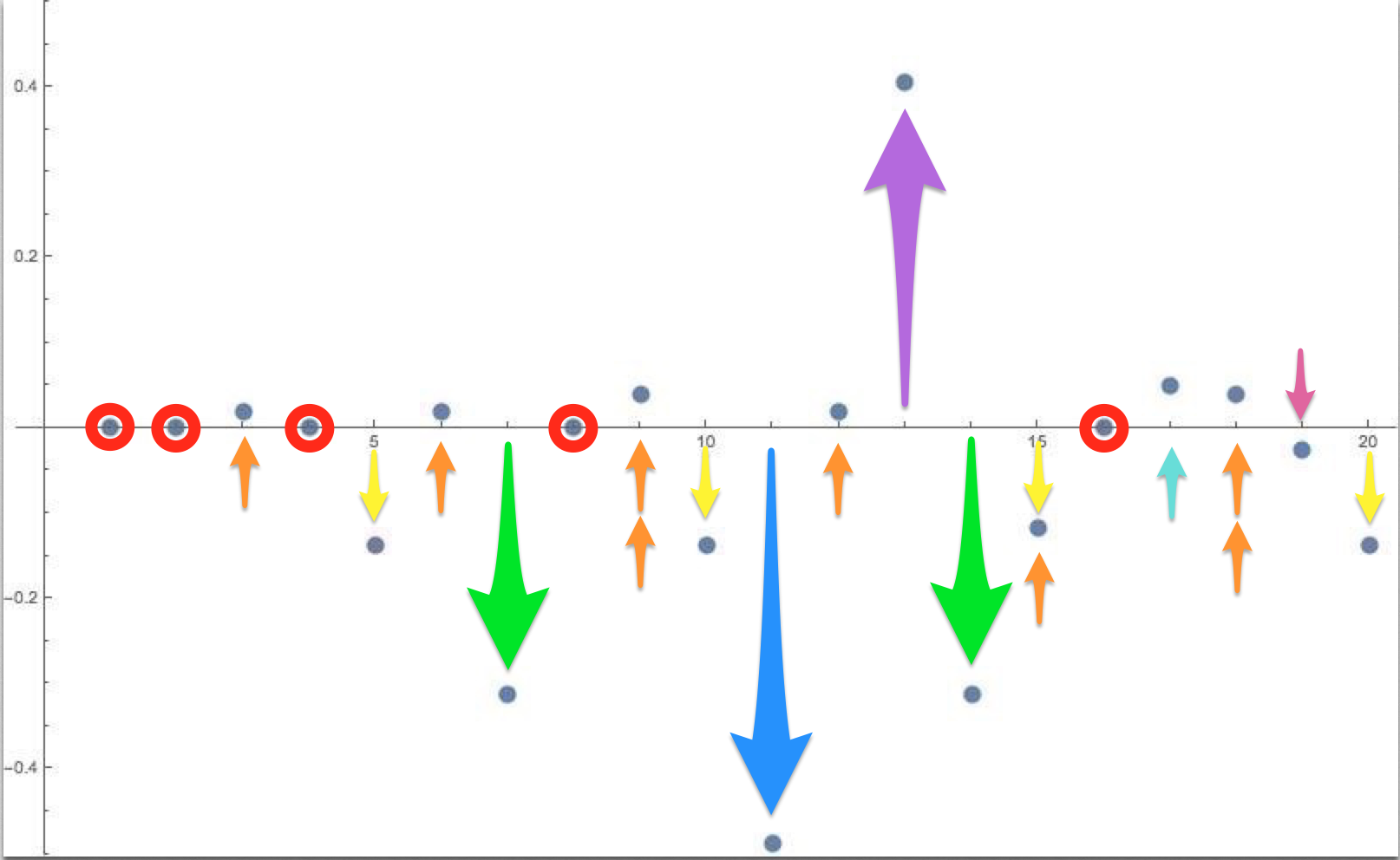
The X-axis names the harmonic number (ending at the 20th harmonic) and the Y-axis is the deviation from the nearest even-tempered note (where for example -0.2 is 20% of a semitone flatter than equal temperament). If you look carefully, you’ll see that the fundamental and all the octave equivalents (harmonic numbers 1,2,4,8, 16 etc.) align perfectly with the even-tempered equivalents. In fact these powers of 2 are the only point where the harmonic series meets up (exactly) with 12-TET. These points are circled in red below.

The ‘non-octave’ harmonics are indicated with different coloured arrows (showing in which way they differ from equal temperament). The 3rd harmonic (indicated in orange) is about 2 cents (a mere 2% of a semitone) sharper than the equal tempered equivalent (a perfect 5th), and so of course are its octave equivalents the 6th, 12th, 24th etc. The 9th harmonic is about 4 cents sharper (as it is ‘affected’ by two 3rd harmonics), and is indicated with 2 orange arrows. This ‘stacking’ (and unstacking) of the 3rd harmonic is what is used to create the Pythagorean scale, also known as a 3-limit scale, since we only allow the 3rd (and 2nd) harmonic as tools to reach musical notes.

The 5th harmonic is significantly flatter than the 12-TET equivalent (and the cause of the many historical temperaments that have emerged in polyphonic music. The 10th harmonic has the same ≈14 cents discrepancy. The 15th ends up about being 12 cents flatter, since 15 = 3*5, it uses the 3rd harmonic (which makes it ≈2 cents sharper than 12-TET) and the 5th harmonic (≈14 cents flatter) resulting in an overall drop of about 12 cents (note the contrary orange and yellow arrows). Incidentally, the use of the 3rd and 5th harmonic (together with the trivial 2nd harmonic), creates the 5-limit system of tuning, with its extensive and beautiful use in Hindustani music.

You’ll see that the other prime-numbered harmonics get their own coloured arrows (7th=green, 11th = blue, 13th = purple etc.). The 11th is about as far from 12-TET that is possible, which is why Harry Partch stops there in his 11-limit 43-note universe. Since the primes never end so the harmonic pathways of tuning are (theoretically) endless.

Another way to see the relationship between the harmonic series and 12-TET is to visualise the harmonics resting at points on an infinitely expanding spiral. Each sweep of the spiral represents an octave, and the 12 equally spaced slices of the octave pizza represent each 12-tone slice. This has the advantage of indicating where in the octave each harmonic lies, as well as the octave relationships between sets of harmonics (e.g. between the 3rd ,6th, 12th and 24th harmonics  etc.). Here’s a beautiful rendering by Skye Lofander (whose website musicpatterns.dk has many awesome visualitions of musical concepts and is highly recommended).

You’ll notice that the harmonics get closer and closer together, and essentially ‘sweep’ through the 12-TET discrepancy in an ever (but never completely) flattening upward slope. Here’s Dean’s rendering which shows the same phenomenon emerging with the first 500 harmonics:

So along the way the 12-TET and harmonic series will get ‘close enough’ most certainly for human perception (which is a couple of cents on a good day) and acoustic instruments (which waver considerably in temperature and human execution). Even a slight head-turn will invoke enough doppler shift to make fractions of a cent meaningless in real terms.

So which is ‘better’ 12-TET or tuning derived from the harmonic series (also known as just (i.e. ‘true’) intonation)? And what incantation of the harmonic series is more ‘pure’? Is 4 jumps up the 3rd harmonic more ‘natural’ than one jump up the 5th harmonic? They both roughly approximate the major 3rd (the first a ‘Pythagorean third’ ≈8 cents sharper than 12-TET, the second a ‘just 3rd’ at ≈14 cents flatter). Some have attempted a measure of harmonicity (see Vals and Monzos), but its relationship to subjective experience is sketchy at best. Can one think of 12-TET as existing way, way up the harmonic series (so still harmonic), is it a ‘good enough fit’, or wholly incompatible with the harmonic series? What’s inate and wha’t encultered? Why 12 equal divisions and why not some other number?

Just intonation enthusiasts can get heated about its superiority to 12-TET, but there is no doubt that the limiting of notes to 12, close-to, or exactly evenly-spaced has led to the creation of countless, otherwise impossible, musical creations and activities.

The best answer is that they are different, and both available to every composer, get over it, embrace and enjoy.

P.S. this was 3 times longer than planned. Apologies.