UPDATE- Since the publication of Brad Osborn’s Kid Algebra (2014), I’m going to switch to his category of Euclidean rhythms (in their 4 types) to describe the patterns below. In summary, Euclidean rhythms (ER) are rhythms in which k onsets in n divisions are as similar as possible, which essentially means that they will only differ by at most one subdivision each. So in ER the groups are as similar as possible, but the term maximally even we will reserve for ER rhythms where the smaller note groups are as separated as much as possible. For example, (2,2,3,3) and (2,3,2,3) are both ER, but only the latter is maximally even.
This is a library of all the maximally even (including strictly even) rhythms for 2-7 rhythmic onsets within 6,8,12 and 16 beat cycles.
Maximal evenness (M.E.) describes a rhythm which is as evenly spread out as possible given both a number or events (rhythmic onsets), and a number of available slots (beats). Strict evenness (marked with a º) is a subset of M.E. and occurs when the hits are equally spaced. M.E. rhythms are intrinsic to much music making in a wide range of cultures from Sub-saharan Africa, South America to EDM and much in between.
The parenthesised number shows the number of displacements (or ‘rotations’) available for the rhythm in the beat-cycle, and allows for starting on rests. When the number of rotations equals the number of beats in the cycle this is marked with an * and represents maximally independence (MI – a common trait of African timelines and clave patterns). Note that 5,6 and 7 in 12 also represents maximally even pentatonic, hexatonic and heptatonic scale sets e.g. 3,3,2,2,2 represents all the modes of the major pentatonic as well as a 5 in 12 set of ME rhythms. As another example 2,2,1,2,2,1,2 (a rotation of 2,2,2,1,2,2,1) represents both the African standard time-line and the Mixolydian mode. Enjoy.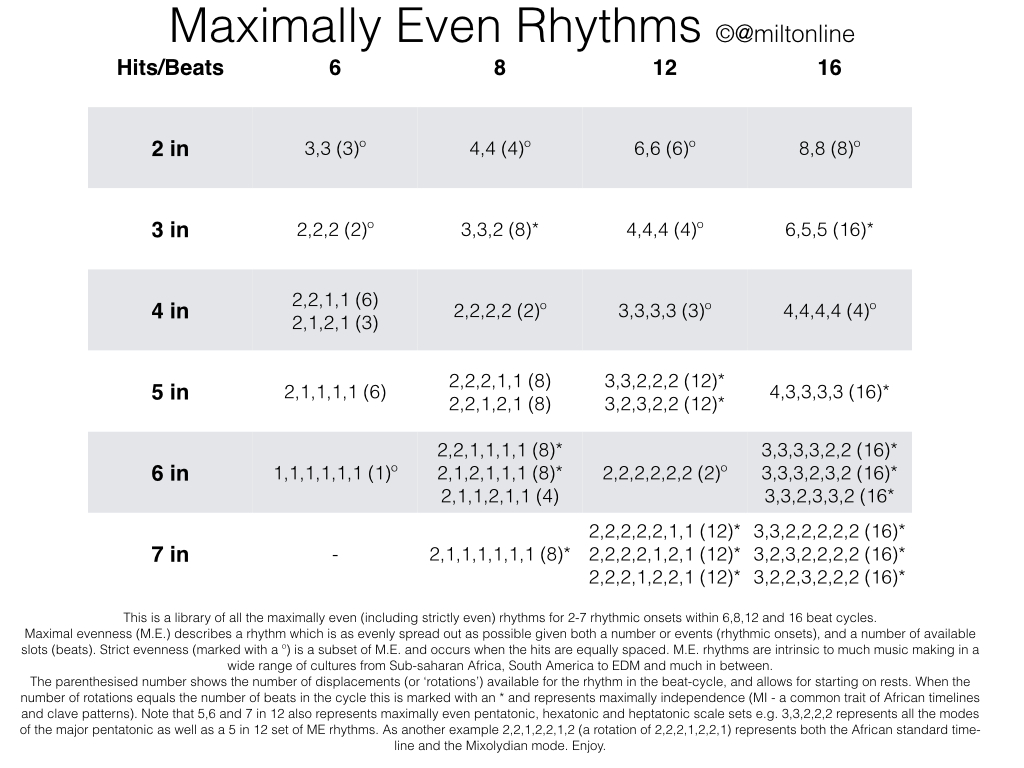

2 replies on “Maximally Even Library”
Glad to see that my clarification (max even vs. Euclidean) has made enough sense as to stick!
Thanks for the comment Professor Osborn, and Your paper is brilliant! I use your system in composition lessons, and also apply the ER types to scale construction. In relation to ME, I see it that type 1 and type 4 ER are necessarily ME, while only one ordering (or its rotations) of type 2 and 3 are maximally even. I can now retire.